50. Etude de fiabilité (Poisson)
Une entreprise mentionne que le nombre de défaillances d'un composant électronique est distribué selon une loi de Poisson au taux moyen de 3 défaillances par 100000 heures.
Outil logiciel : SE_exe-modeles.exe[1]
Question
On souhaite étudier la consommation attendue de cette pièce sur 20000 heures (environ 2 ans de fonctionnement en continu)
Calculer le paramètre m de la la loi de Poisson à partir du taux d'arrivée λ=3/100000 h-1.
Indice
Sur période dt, le nombre moyen d'événements est m=λ.dt
Solution
m= 3*20000/100000=0,6 défaillances en moyenne sur la période de 20000 heures
Question
Quelle est la probabilité d'obtenir 1 défaillance pendant 20000 heures.
Utilisez le programme Modèles statistiques (exécutable), choisir le modèle ou loi de Poisson.
Renseignez m=0,6. Le programme calcule les probabilités d'un nombre d'événements de 0 à k max. Pour être assuré que les cas possibles sont représentés, vérifier que F(k max)=P(X<=k max) soit proche de 1.
Solution
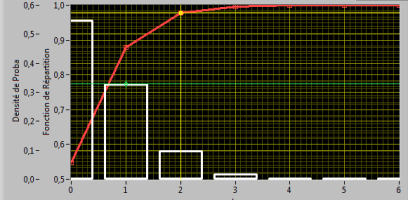
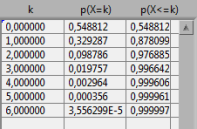
Sur une période de 20.000 heures on peut s'attendre à obtenir 0,6 défaillances (3 * 20.000 / 100.000) en moyenne.
La variable étudiée est X : "Nombre de pannes sur 20.000 heures".
D'après la loi de poisson, on a donc E(X)=0,6 défaillance et V(X) = 0,6
Les cas les plus probables seront donc 0 ou 1 défaillance sur 20.000 heures.
Les calculs donnent une probabilité p(X=1) de 32,93 % d'obtenir exactement 1 et 1 seule défaillance.
Question
Quelle est la probabilité d'obtenir au moins 2 défaillances. Exprimez cette probabilité en fonction de F(X=k) = prob (X<=k).
Indice
Si E est l'événement "au moins 2 défaillances" (X=2 ou X=3 ou X=4 ..... ou X=∞)
alors {non E} est "moins de 1 défaillance". prob(X>=2)=1- prob(X<=1)=1 -F(X=1)
Solution
On a donc p(E) =p( X >= 2) = 1-F(X=1) ou encore 1-p(X=0)-p(X=1)
soit une probabilité de 12,2% d'obtenir au moins 2 défaillances --> p(X>1) = 1-p(X=0)-p(X=1) avec p(X=0)=54,9% et p(X=1) de 32,93 %
Question
Dans le cadre d'une gestion de stock, on peut estimer les 20000 heures à 2 ans de fonctionnement en continu.
Si on décide de stocker 1 pièce en sécurité, quelle est la probabilité de ne pas utiliser cette pièce pendant les 2 années.
Cette probabilité donne une idée du coût de possession[2] (maintien en stock d'une pièce inutilisée).
Solution
On a p(X=0)= 54,9%, soit un peu plus d'une chance sur 2 de conserver la pièce plus de trois ans en stock.
Ce risque est à comparer à la pénalité encourue d'avoir à commander cette pièce en urgence en cas de besoin.