Caractéristiques de la Fiabilité

DéfinitionFiabilité

Pré-requis : Fiabilité

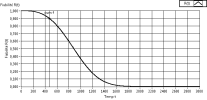
La fiabilité d'un dispositif au bout d'un temps t correspond à la probabilité pour ce dispositif de ne pas avoir eu de défaillance entre 0 et t.

Pré-requis : Observations statistiques

Les études vont porter sur l'étude d'une variable aléatoire T

Fiabilité R(t)

R ( t ) = Prob ( T > t ) R(t)=Prob(T>t)

Fonction de répartition des défaillances F(t)

F ( t ) = Prob ( T < t ) = 1 − R ( t ) func F(t)=Prob(T<t)=1 - func R(t)

il en résulte que :

  • R(t) est une fonction décroissante de t sur [0,∞[.

  • R(0)=1 et R(∞)=0

ExempleGraphe de R(t)

Représentation de R(t) selon le modèle de Weibull

Modèle de Weibull. Fiabilité

DéfinitionDensité de probabilité des défaillances

f(t) en fonction de R(t)

f ( t ) = dF ( t ) dt = − dR ( t ) dt f(t)={dF(t)} over {dt}=-{dR(t)} over {dt}

R(t) en fonction de f(t)

R ( t ) = 1 − ∫ 0 t f ( t ) . dt R(t)=1-int from{0} to{t} f(t).dt

A l'aide de la densité de probabilité, si N dispositifs non réparables sont en fonctionnement à t=0 alors la proportion de défaillances attendues entre t et t+dt est de dN(t)=N.f(t).dt

DéfinitionMTTF

Espérance mathématique de la variable aléatoire T

Espérance mathématique de la variable aléatoire T

MTTF = E ( t ) = ∫ 0 + ∞ t . f ( t ) . dt MTTF=E(t)=int from{0} to {+ infinity } t.f(t).dt

DéfinitionTaux de défaillance

λ(t).dt représente la probabilité conditionnelle qu'une défaillance du dispositif se produise entre t et t+dt sachant que ce dispositif n'est pas tombé en panne avant t.

λ ( t ) = − 1 R ( t ) . dR ( t ) dt %lambda(t)=-{1} over {R(t)}.{dR(t)} over {dt}